傾向線②:その傾向線、本当に使って大丈夫??
Nanaeです。こんにちは。傾向線第2弾で、今回は統計側の話題です。行と列に連続値が入っているチャート、例えば散布図なんかを作ったら、Tableauではドラッグアンドドロップだけで傾向線を引けますよね。傾向線は一瞬で上がり下がりの傾向がわかるのでよく使われる方も多いと思います。そのとき、傾向線の傾きだけですぐに「これは正の相関だな!」とすぐに解釈してませんか!?それ、実は危険かもしれません。そこで今回は、傾向線を引いたときにTableauが出してくれる線や値から、その傾向線を使っても問題ないのか確認してみましょう。
まず、傾向線って何でしょうか。ある変数yを他の変数xによって計算するためのモデルのことです。傾向線をマウスオーバーするとy=ax+bという形で計算式が出てきますよね、傾向線はあの式を描いています。下の例では、yが売上、xが数量で、数量が1個増えると、売上は6349.79円増えるということを意味しています。

でもその傾向線から何かの情報を得る前に、その傾向線をそもそも使っていいのか確認しておく必要があります。傾向線をマウスオーバーすると、式と一緒にR-2乗とP値という値が出てきます。ここが見てほしいポイントです。結論としては、以下2点を満たしているかチェックしてください!ざっくりとした目安になります。
① R-2乗が0.5や0.6程度より大きければOK
② p値が0に近ければOK
① R-2乗(アールじじょう):データがどの程度モデルから説明されているか?
決定係数とか寄与率と呼ばれます。モデルとデータの関係をみたとき、このモデルはどの程度データを決定(=説明)しているのか、寄与しているか、を表しています。0~1の値を取るもので、値が大きいほどデータはモデルで説明されているよいモデルであり、そのとき各マークは傾向線の近くに集まります。逆に0に近ければ、傾向線とは関係なく散らばります。
じゃあR-2乗がいくつ以上であれば十分だと判断していいか、肝心なところがきっちりと決まっているわけではありませんが、0.5とか0.6より大きければ役に立つと言われています。
② p値(ピーち):その傾向線は偶然できたもの?信頼できるもの?
possibilityのpで、有意確率と呼ばれます。p値が低ければ、この傾向線は偶然ではなく、同じ条件の他のデータで傾向線を出しても、似たような線が得られると考えることができます。
ちなみに、値が小さいほうが良いわけは、こんな流れで考えています。p値とはこのモデルが成立しない確率です。その確率がとても低いってことは、このモデルは偶然できたものではなく意味があるだろう(意味が有る→有意)。という流れです。
ということで、p値というのは、ただの偶然出てきたわけではないことを確認していたんですね。p値は5%か1%より小さければOKです。
まずは傾向線と一緒に出てくるR-2乗とp値の2つを意識すると、より正しく傾向線を扱えるようになると思います!
---Advanced---
さらにもう一歩進めるには、各マークと回帰モデルのズレ(=残差)に偏りがないかも確認したほうがいいです。
残差のデータを得るために、Desktopのメニューから、ワークシート→エクスポート→データ(MSのアクセスファイルになります)に接続します。

ここに入っているデータは、散布図で使った、売上と数量、それから、モデルから算出された予測値と残差です。
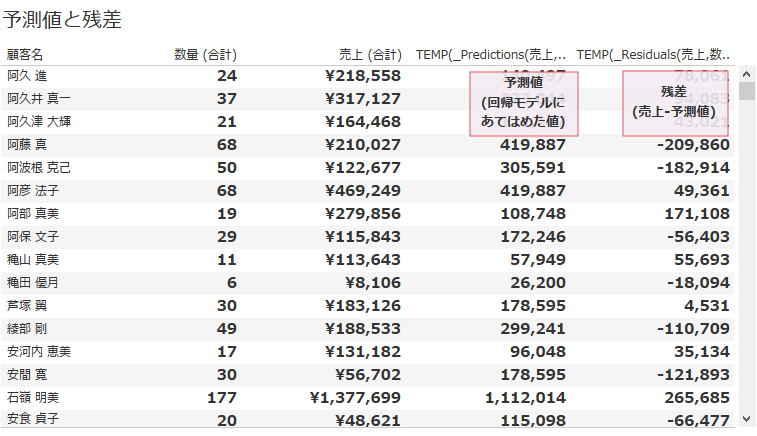
この残差が0付近に集中して均等に散らばっていればOKです。どのマークでもモデルとのズレが均等であれば、そのズレは誤差と考えることができるので、このモデルはあてはまりがよかったんだなといえます。
均等にばらついているかみるために残差と数量の散布図と、残差が0付近に集中しているかみるためのヒストグラムを作成しました。

散布図からは、数量が大きくなればなるほど0から遠い位置でプロットされてしまっていることがわかります。よって、数量が少ないときはまだ使えるかもしれないけど、数量が多いときは信頼感に欠けることが読み取れます。理想は、数量がいくつであっても0付近に分布するような散布図です。
ヒストグラムからは0付近に多く出現しているので、OKです。
さらに、実際の売上と、モデルから算出された予測値が近いかどうかも見てみるために、実際の売上と算出された売上を散布図で表しました。y=xすなわち左下から右上に対角線で分布しているので、まぁまぁ予測できていますが、売上が大きくなるにつれて分散が大きくなっていることが読み取れます。もしも予測値が売上とが完全に一致していれば、対角線上にのみプロットされます。

傾向線シリーズ第2弾では、
前半で、
R-2乗から、傾向線はこのデータをうまく説明してるよね?
p値から、たまたま出てきた再現性のない傾向線ではないよね?
後半で、
残差から、モデルの値と実際の値との差は誤差として考えていいんだよね?
ということを確認しました。
気軽に出せる傾向線が、その分析で使うのに本当に適切なのかを判断する方法のご紹介でした!
Nanae












0 コメント: